یکی از مسائل لاینحل ریاضی حل شد

پس از چند دهه که یک مسئله مهم و دشوار ریاضی لاینحل باقی‌مانده بود، راه‌حلی برای آن ارائه شد. از سال ۱۹۵۰ میلادی تاکنون مسئله ریاضی مشهور به هادویگر – نلسون (Hadwiger-Nelson problem) که توسط هوگو هادویگر (Hugo Hadwiger) و ادوارد نلسون (Edward Nelson) مطرح‌شده بود، بدون راه‌حل مناسب باقی‌مانده و هیچ‌کس نتوانسته بود این مسئله را حل کند تا اینکه به‌تازگی این مسئله به شکل بسیار شگفت‌انگیزی حل شد.

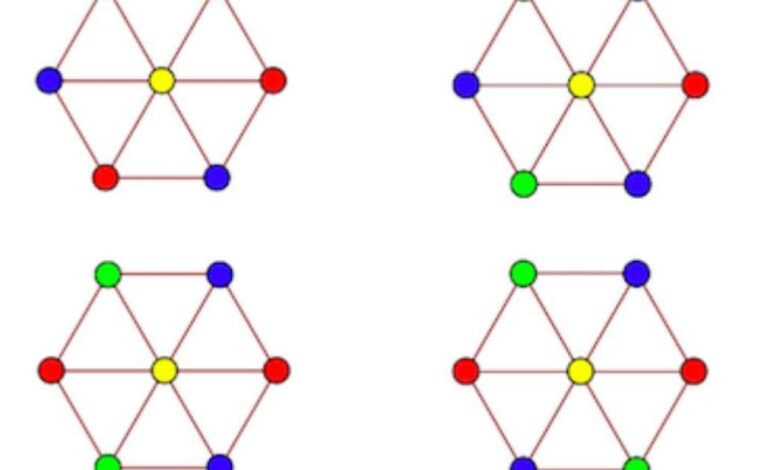
کشف راه‌حل این مسئله ریاضی با بازی موسر اسپیندل (Moser spindle) انجام شده و در آن از یک الگو با ۷ نقطه و ۱۱ لبه استفاده شده است. دی گری با استفاده از نرم‌افزار کامپیوتری، به کپی نسخه موسر اسپیندل پرداخته و یک شبکه گسترده از ۲۰۴۲۵ نقاط اتصال را ایجاد کرد. سپس او با کمک قواعد بازی توانست پیدا کند که حداقل ۵ رنگ برای رنگ‌آمیزی تمام نقاط صفحه نیاز است به‌طوری‌که هیچ دونقطه در فاصله یک واحد از یکدیگر رنگ یکسان نداشته باشند.

قابل‌توجه است که این مسئله توسط یک ریاضیدان حل‌نشده بلکه فردی که موفق به حل این مسئله شده یک متخصص زیست‌شناس رایانه‌ای بریتانیایی (computer scientist-turned-biologist) است که بیشتر انرژی و تلاش خود را صرف طراحی درمان برای پیری کرده است.

اوبری دی گری (Aubrey de Grey) اخیراً موفق به حل این معضل ریاضی که چندین دهه گذشته لاینحل باقی‌مانده بود، شده و در مقاله‌ای با عنوان The Chromatic Number of the Plane is at least ۵ به شرح آن پرداخته است. لازم به ذکر است که این مقاله هنوز به‌طور مستقل موردبررسی قرار نگرفته اما در سایت arXiv منتشرشده است.

این معمای ریاضی به نظر می‌رسد که نسبتاً آسان و ساده بوده اما تقریباً برای ۷۰ سال ریاضیدانان حرفه‌ای جهان را درگیر خودکرده بود و آن‌ها نتوانسته بودند در این مدت آن را حل کنند. مسئله ریاضی هادویگر – نلسون می‌پرسد که حداقل تعداد رنگ موردنیاز برای رنگ‌آمیزی صفحه به‌طوری‌که هیچ دونقطه در فاصله یک واحد از یکدیگر رنگ یکسان نداشته باشند، چندرنگ است؟ پاسخ تاکنون نامشخص بوده اما به یکی از اعداد ۴، ۵، ۶ و یا ۷ محدود می‌شده است.

دی گری در مقاله خود نشان داده که در یک صفحه تمام نقاط را نمی‌توان با چهار رنگ متفاوت رنگ کرد؛ بنابراین حداقل تعداد رنگ موردنیاز پنج است. با توجه به این‌که ریاضیدانان در طول ۷ دهه با این مشکل روبرو بوده و نتوانسته بودند آن را حل کنند، حل این مسئله یک پیشرفت بزرگ محسوب می‌شود.

کشف راه‌حل این مسئله ریاضی با بازی موسر اسپیندل (Moser spindle) انجام شده و از یک الگو با ۷ نقطه و ۱۱ لبه استفاده شده است. دی گری با استفاده از نرم‌افزار کامپیوتری، به کپی نسخه موسر اسپیندل پرداخته و یک شبکه گسترده از ۲۰۴۲۵ نقاط اتصال را ایجاد کرد. سپس او با کمک قواعد بازی توانست پیدا کند که حداقل ۵ رنگ برای رنگ‌آمیزی تمام نقاط صفحه نیاز است به‌طوری‌که هیچ دونقطه در فاصله یک واحد از یکدیگر رنگ یکسان نداشته باشند.

دی گری معتقد است که بسیار خوش‌شانس بوده چراکه پس از تقریباً ۷۰ سال تنها فردی بوده که توانسته این مسئله را حل کند. این دانشمند ۵۵ ساله ادعا می‌کند که انسان توانایی زندگی کردن هزارساله را دارد. این ادعا بسیار جسورانه بوده و حتماً منتقدانش سکوت نخواهند کرد اما او همچنان به فعالیت‌های خود در رابطه با تحقیق، انتشار و تبلیغ برخی از پیشگام‌ترین داروهای احیاکننده در جهان ادامه می‌دهد.

ترجمه: فاطمه کردی

منبع: iflscience

No tags for this post.