حل یک معمای ریاضی ۶۰ ساله
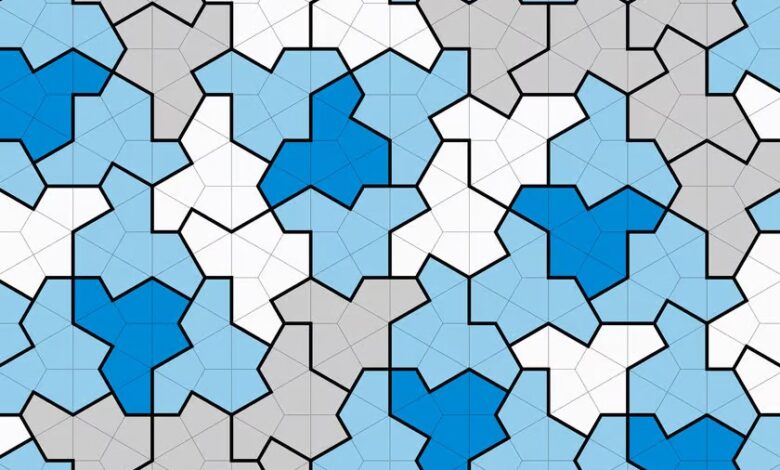
شکل جدیدی کشف شده است که می تواند مجموعه ای منحصر به فرد از کاشی ها را ایجاد کند. این شکل ۱۳ وجهی که با نام مستعار کلاه شناخته می شود، می تواند بدون تکرار یک الگو، با خود یک معمای ریاضی ۶۰ ساله را حل کند.
به گزارش سیناپرس، این نقطه عطف بسیار مهم توسط دیوید اسمیت (David Smith) یکی از علاقه مندان به کاشی کاری از یورکشایر، انگلستان امکان پذیر شد. اسمیت همراه با بسیاری از افراد دیگر در جامعه، به دنبال نوع خاصی از شکل به نام تکتک دورافتاده یا انیشتین بود. این نام هیچ ربطی به فیزیکدان معروف ندارد، بلکه در عوض بازی با کلمات آلمانی ein (به معنی یک) و stein (به معنی سنگ) است.
شکل یک سنگ یک شکل فرضی سابق است که می توانست هواپیما را بدون هیچ همپوشانی یا شکافی کاشی کند و حتی اگر در فضایی بینهایت کشیده شود، هرگز همان الگو را تکرار نمی کند و کلاه اسمیت اولین شکلی است که متناسب با آن است.
ممکن است برای بسیاری از مردم چندان مهم به نظر نرسد، اما ریاضیدانان از اواسط دهه ۱۹۶۰ به دنبال یک قطعه پازل با این ویژگی ها بودند. در آن زمان بود که اولین مجموعه از اشکال برای نمایش کاشی کاری های دوره ای غیر تکراری کشف شد، اما جعبه ابزار به بیش از ۲۰ هزار شکل مختلف نیاز داشت تا اطمینان حاصل شود که الگو هرگز تکرار نمی شود. کار بیشتر در دهه بعد این تعداد را کوچکتر و کوچکتر کرد تا اینکه سر راجر پنروز ترتیباتی را شکل داد که اکنون به عنوان کاشی کاری پنروز شناخته می شوند.
پروفسور کریگ کاپلان (Craig Kaplan) محققی در مطالعه ای که شکل جدید را توصیف می کند، گفت: این دو شکل در محلول پنروز ساختار کافی داشتند که تناوب را ممنوع می کردند. اما تقریباً ۵۰ سال است که ریاضیدانان از خود می پرسند، آیا می توانیم این کار را با یک مونوتل انجام دهیم؟
اسمیت در ابتدا با برش های کاغذی اشکال مختلف را آزمایش می کرد. برای تأیید توانایی های ویژه شکل موسوم به کلاه، او با کاپلان که اخیراً نرمافزاری را توسعه داده بود که می توانست یک شکل مشخص را در مقیاسهای بزرگتر بررسی کند، تماس گرفته و سپس بررسی کرد که آیا این شکل ها می توانند در یک کاشی کاری بزرگتر بدون نقض قوانین وجود داشته باشند یا خیر.
به گزارش سیناپرس، شکل کلاه نیز ممکن است تنها شکل تک تک دوره ای ممکن نباشد. این تیم تحقیقاتی می گوید که از نظر فنی، بخشی از خانواده ای از اشکال بسیار مشابه با تغییرات جزئی است که همچنان از همان قوانین پیروی می کنند.
شرح کامل تحقیقاتی که شکل جدید را توصیف می کند در مجله ArXiv منتشر شده است.
مترجم: فاطمه امینی

