از زنان علمی جهان کم شد
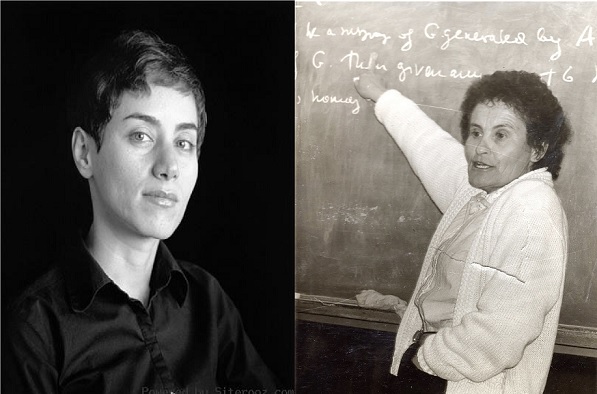
امی ویلکینسون (Amie Wilkinson)، ریاضیدان آمریکایی، در این مقاله با اشاره به درگذشت دو بانوی ریاضیدان می نویسد: بخش ریاضی آکادمی ملی علوم آمریکا فهرستی از 104 عضو این بخش را منتشر کرد. در این فهرست تنها نام 4 زن دیده می شود؛ درحالیکه این آمار تا دو ماه پیش 6 نفر بود.
مریم میرزاخانی (Marayam Mirzakhani): ستاره جوان ایرانی (دانش آموخته دانشگاه صنعتی شریف) و استاد دانشگاه استنفورد 15 ژوئیه (24 تیر) بدلیل ابتلا به سرطان در سن 40 سالگی درگذشت. میرزاخانی نخستین بانوی ریاضیدان جهان بود که موفق به کسب مدال معتبر فیلدز (Fields Medal) شد.

(تصویر: France-Presse)
ویلکینسون می نویسد: نخستین بار، زمانی که فارغ التحصیل شده بودم، نام میرزاخانی را شنیدم. وی، فرمول جدیدی برای توصیف منحنی روی سطوح انتزاعی خاص ارائه کرده بود و این تحقیق، پیامدهای مهمی در پی داشت؛ به عنوان مثال، اثبات جدید حدس معروف در فیزیک در خصوص گرانش کوانتومی.
مارتینا راتنر (Martina Ratner): ریاضیدان متولد اتحاد جماهیر شوروی سابق و دانش آموخته دانشگاه کالیفرنیا در برکلی، اوایل ژوئیه سال جاری در سن 78 سالگی درگذشت.
موفقیت راتنر در علم ریاضی، به دهه 50 عمر وی و انتشار نتایج تحقیقات وی موسوم به قضیه راتنر (Ratner’s Theorems) بازمی گردد. این نتایج، گشفت انگیز و به طور گسترده ای قابل استفاده بودند.

(تصویر: Anna Ratner)
ویلکینسون در ادامه می نویسد: من از این دو بانوی ریاضیدان الهام گرفتم. فعالیت آنها بسیار به هم نزدیک و به برخی از قدیمی ترین سوالات در ریاضیات مرتبط بودند.
یونانیان باستان مجذوب جامد افلاطونی (Platonic solid) – یک شکل سه بعدی که با چسباندن قطعات مسطح همانند در یک روش یکسان ساخته می شود – بودند. قطعات باید چند ضلعی های منظمی با طول و و زوایای برابر باشند؛ به عنوان مثال، مکعب یک جامد افلاطونی ساخته شده از 6 مربع است.
با توجه به تعریف موجود، به نظر می رسد که وجود بی نهایت جامد افلاطونی امکانپذیر است، درحالیکه تنها 5 نمونه (مکعب، چهارضلعی، هشت وجهی، دوازده وجهی و بیست وجهی) وجود دارند. این قضیه توسط ریاضیدان یونان باستان، تئتتوس (Theaetetus) اثبات شد.
چیزی که سخت و مستحکم است، بدون از بین بردن ماهیت اساسی، تغییر شکل پیدا نکرده یا خمیده نمی شود. برخی اوقات اشیاء نظری (theoretical objects) نیز می توانند بقدری سخت باشند که وجود نداشته باشند (mathematical unicorns).
در استفاده معمول، الماس قدرت خود را مدیون استحکام ساختار مولکولی است؛ استحکام کنترل شده – انعطاف و خمیدگی در جهت های خاص – این امکان را برای پل های معلق فراهم می سازد تا در برابر بادهای شدید مقاومت کنند.
دکتر میرزاخانی و دکتر راتنر، متخصص فرم ظریف تری از این استحکام و سختی (rigidity) بودند. این دو ریاضیدان بدنبال توصیف اشکال در فضاهایی با بعد بالاتر بودند.
یک مثال موجود، مدل ریاضیاتی موسوم به دانه برف کخ (Koch snowflake) است که شامل الگوی تکرارشونده مثلث در امتداد لبه آن است. لبه این دانه برف در هر مقیاسی که مشاهده شود، یکسان است. دانه برف با هر تغییر شکل، به طور اساسی تغییر نمی کند.

نتایج تحقیقات این دو ریاضیدان بسیار وسیع هستند: نتایج تحقیقات دکتر راتنر به توسعه ابزاری منجر شد که طیف گسترده ای از کاربردها از جمله توصیف بلوک های سازنده اساسی در هندسه جبر را شامل می شود.
تحقیقات دکتر میرزاخانی با همکاری دکتر الکس اسکین که magic wand theorem نامیده می شود نیز کاربردهای مختلفی از جمله مدل درخت- باد (wind-tree model) دارد.
همچنان زنان مستعد دیگری در جهان وجود دارند که بدنبال یافتن پاسخ برای سوالات اساسی هستند، اما چرا تعداد آنها زیاد نیست؟
مترجم: معصومه سوهانی
منبع: nytimes

